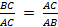terug naar beginpagina

gulden snede

laats bijgewerkt 14-08-2016

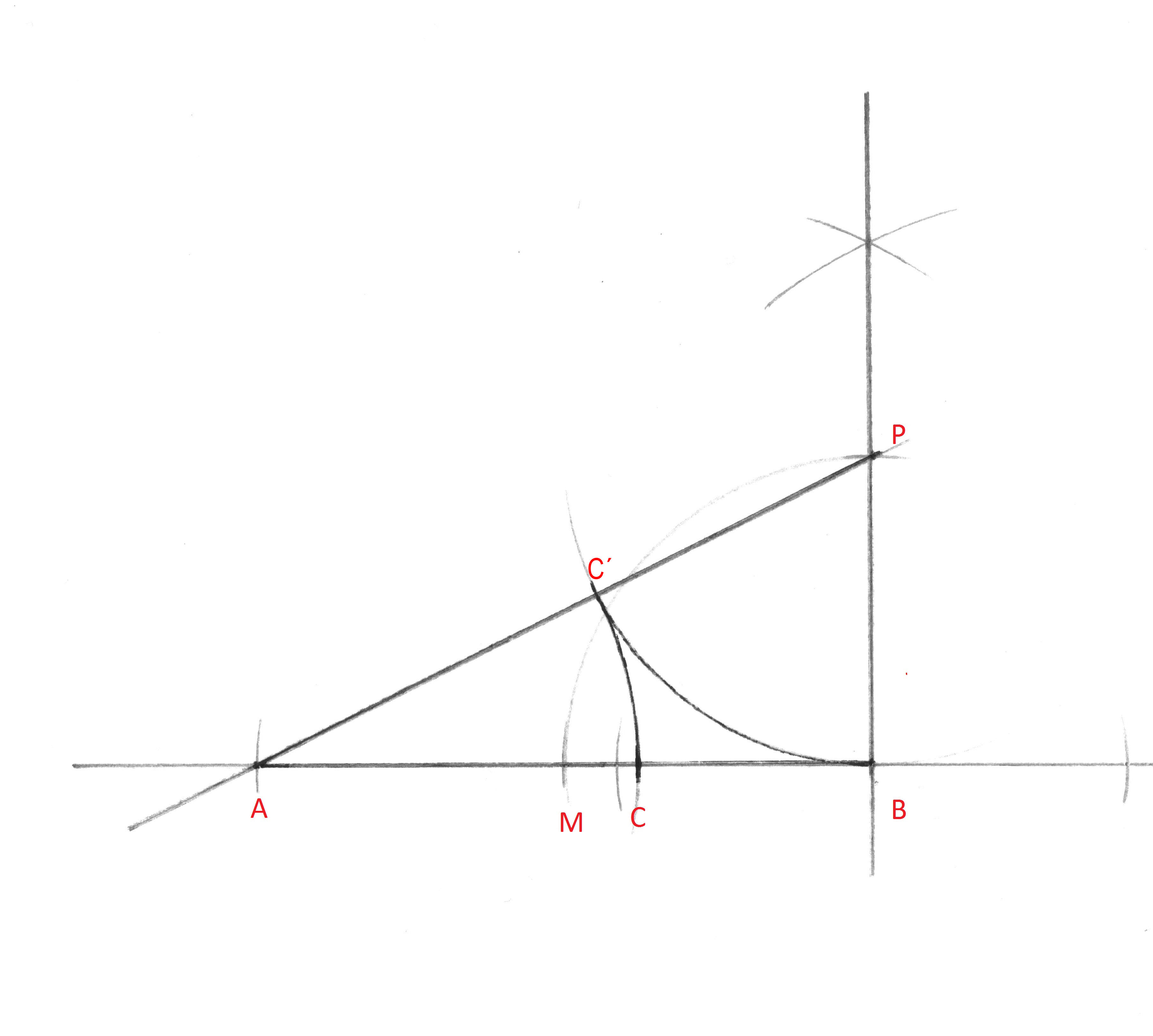
De gulden snede is een verdeling van de lijn AB in twee delen zodanig dat:

Met bovenstaande constructie wordt het lijnstuk als zodanig verdeeld.

- teken een rechte lijn,

- neem een punt B op de lijn

- richt een loodlijn op in B

- neem op de loodlijn een punt P

- cirkel Met middelpunt B, BP om naar de beginlijn en vind M

- zet BP uit op de lijn vanuit M en vind A

Dit kan natuurlijk ook anders maar nu heb je een rechthoekige driehoek ABP

Lange rechthoekszijde is tweemaal korte rechthoekszijde

- cirkel met middelpunt P, PB om naar PA , vind punt C’op PA

- cirkel met middelpunt A de afstand AC’ om naar AB en vind C

Hiermee is de lijn verdeeld volgens de gulden snede.

Bewijs:

BP = 1

dan AB = 2

pythagoras: 1² + 2² = AP²

                                   AP = √ (1² + 2²) =  √5 .

[Het betreft hier de lengte van het lijnstuk AP.

Er is dus slechts één, positief, antwoord]

AP = √5

PC’ = PB = 1

AC = AC’ = AP – PC’ = AP – 1 = √5 – 1

AB = 2

BC = AB – AC = 2  – (√5 – 1) = 3 – √5

AB × BC = 2 × (3 – √5)                    = 6 – 2√5

AC × AC = (√5 – 1) × (√5 – 1)         = 6 – 2√5

AB × BC = AC × AC

of anders geschreven:  

dit maakt de volgende berekening mogelijk:

 =    ≝ φ = 0,6180339887

[voor de verhouding AC/BC=AB/AC    ≝     Φ  =   1,6180339.. ]

dus als AC bekend dan BC te berekenen

en als BC bekend dan AC te berekenen

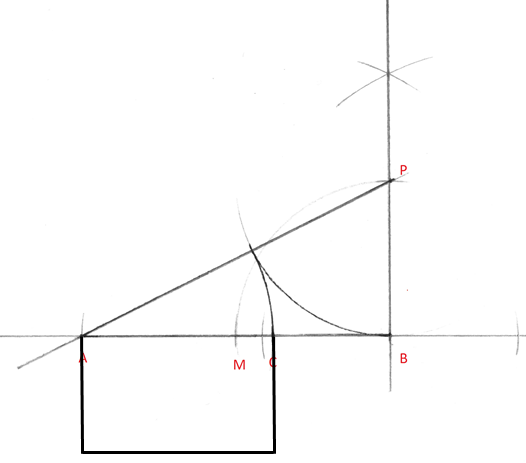
bijvoorbeeld

als AC = 2,97 cm

dan kruislings vermenigvuldigen.                  BC × 1 = AC × φ

                                                                       BC = 2,97 × 0,6180339887 = 1,83556 cm

wat de volgende rechthoek oplevert die zijden heeft

volgens de gulden snede:

Vergelijk de constructie

deze rechthoek is in de zelfde verhouding als al geconstrueerd hierboven

Een rechthoek in de verhouding van de gulden snede,

[bijvoorbeeld met een bepaald oppervlak en met een vastgestelde lengte van één van de zijden],

maakt deel uit van een serie op de volgende manier:

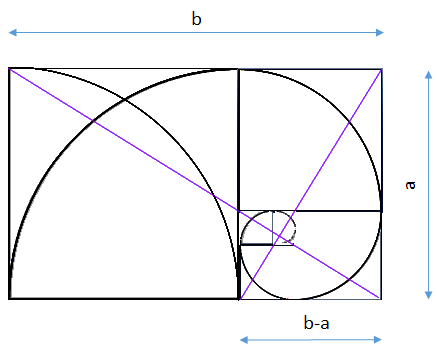
 Bovenstaande rechthoek is in de verhouding van de gulden snede.

dat betekent dat:

de rechthoek met korte zijde b-a en lange zijde a is ook een rechthoek in de verhouding van de gulden snede.

bewijs:

verhouding zijden grote rechthoek

a × (a + b )      = b²

a² + ab             = b²

Trek van de grote rechthoek een vierkant af met zijden a

dan ontstaat een rechthoek met zijden  b-a  en  a.

Als deze rechthoek in de verhouding van de gulden snede is,

dan moeten de zijden in de zelfde verhouding staan

als die van de grote rechthoek met zijden a en b.

   Dit omwerken

b × ( b – a ) = a²

b² – ab        = a²

b²                = a² + ab = a × (a + b )

Wat weer te schrijven valt als:

net als is als de verhouding van de oorspronkelijke rechthoek.

Waarmee de kleine, tweede, rechthoek dus ook in de verhouding van de gulden snede is.

opmerkingen:

- De paarse lijnen zijn de diagonalen van de eerste twee rechthoeken.

Met behulp van deze lijnen kunnen achtereenvolgens alle verdere rechthoeken getekend worden.

- Deze verdeling kan ook mooi gebruikt worden voor het tekenen van

            een krul of overgangsboog.

- De getallen   φ  en  Φ  kunnen niet door breuken vervangen worden.

- Met de rij van Fibonacci kunnen de getallen φ en Φ bij benadering berekend worden.

            Hoe verder in de rij een getallenpaar genomen wordt hoe beter de benadering.

rij van Fibonacci	0	1	1	2	3		5		8			13	21	34				55	89	144	233
n/(n+1)	0/1		1/2		3/5					8/13			21/34			55/89				144/233
		1/1		2/3				5/8			13/21				34/55				89/144
benadering φ	0		0,5		0,6					0,615385			0,617647				0,617978			0,61803
		1		0,66667				0,625			0,619048				0,618182				0,6180556
(n+1)/n	1/0		2/1		5/3					13/8			34/21				89/55			233/144
		1/1		3/2		8/5					21/13				55/34				144/89
benadering Φ			2		1,666667					1.625			1,619048				1,618182			1,6180556
		1		1,5		1,6					1,615385				1,617647				1,617978

Ter vergelijking

Van een rechthoek met A4 formaat staan de zijden in de verhouding 1/√2

neem bijvoorbeeld de korte zijde 21 dan:

lange zijde = 21 × √2 = 29,7

 De A4 rechthoek hieronder met die maten [op schaal] benadert de rechthoek met de verhouding van de gulden snede

A4

De twee figuren over elkaar heen tonen het verschil:

A4 met daaroverheen gulden snede waarbij lengte gelijk aan A4

links:

Er is eindeloos veel op het net te vinden

nederlands: gulden snede

frans: Nombre d'or

duits: Goldener Schnitt

engels: Golden ratio

esperanto: ora proporcio